1 引言

    九十年代以來，市場競爭的不斷加劇、產品的多樣化和更高顧客化需求給企業帶來了很大的壓力，企業越來越意識到在生產過程中引進操作柔性的重要性。一臺SMC插置機器可以通過增加插頭或者在插頭上增加可以插接不同元件的取件器而提高自身的操作柔性。而一條裝配線通常通過安裝不同的插置機器使其能夠生產不同種類的產品類。

    從1990年代以來，關于FMS生產能力調整問題已經有了相當的研究。文獻[2]提出了一個在多產品背景下，多種技術可供選擇時的生產能力擴充模型，正如他在文中所述，這個模型的一個主要的局限在于需求不減的假設和柔性生產能力只生產特定的產品類的假設。文獻[3]研究了在多計劃期多種機器生產單產品類，并且設備規模離散時，生產能力的擴充、縮減以及替換的策略。文獻[4]和文獻[5]研究了生產能力擴充的最優策略，盡管在模型中考慮了剛性設備和柔性設備之間的選擇，但是，他們的模型和求解方法不能直接應用到PWB裝配線問題上，文獻[6]研究了不同計劃期上需求變化且多產品類背景下，剛性設備和完全柔性設備之間的權衡問題。文獻[7]隨后在隨機多種需求情形以及產品生命周期不確定的背景下將其結果進行了擴展．文獻[8]用一類模型來比較在不同的生產環境和控制策略下，產品的多樣性和生產的過程柔性對于生產的影響．這和本文的模型有一定的類似之處，但是要指出的是他們并沒有考慮產品的結構，也就是產品的BOM約束．文獻[9]研究了需求隨時間變化的情形下生產能力的擴充問題，他們以最小化新設備投資成本、設備運作成本和庫存成本為目標，提出了一個多階段的混合整數規劃模型，并且通過Lasransian松弛的方法來尋找有效的新設備投資計劃。文獻[10]考慮了在一系列離散的需求情形下，并在廣定的投資約束下購買新設備，以未滿足需求最小化為目標建立了一個隨機整數規劃模型。他們找到了一個不隨需求變化的購買設備的集合，在該集合中選擇購買設備，可以以最小的投資成本滿足最大的需求．在多計劃期，多產品類，需求確定但會隨不同計劃期發生變化的情況下，文獻[11]提出了一個PWB裝配線能力擴充的模型，該模型考慮了機器的柔性以及產品的BOM約束．文獻[12]在該基礎上擴展到隨機的多種需求情形下的生產能力擴充問題，提出了一種通過求解多個背包問題來分解原問題的方法。但是，文獻[12]只研究了能力擴充問題，而沒有考慮能力縮減以及能力轉移問題，當考慮能力縮減以及能力轉移時，無法用背包問題來描述能力調整，需要開發其他的算法來求解這一問題．本文將研究隨機多種需求情形下的生產能力調整問題，在這種不確定的情形下進行生產能力的調整，將會帶來風險，因此在模型中將加入對于風險的描述，本文提出的求解方法不僅僅解決能力擴充問題，而且還能夠得到完整的能力調整決策(包括設備拆卸以及設備轉移)。

    文章的結構如下：第2節提出了PWB裝配線的一個能力規劃模型；第3節提出了減少搜索空間的一個啟發式算法，得到模型的調整略集；第4節運用遺傳算法對調整略集進行搜索；第5節通過實例驗證了本文方法的正確性和可行性；第6節為文章的結論部分。

2 BOM約束下的能力規劃問題

    本文將要考慮隨機需求下的能力規劃問題，在多個時間段上需求有多種可能情形，在這種不確定的情形下進行生產能力的調整，將會帶來風險，因此在做出能力調整決策時，需要考慮兩個目標，即最大的期望收益和最小的風險．在文獻[13]的FMS能力規劃模型中，運用期權定價的方法描述了風險，本文也將采用這種方法表述風險。

    具體模型眠如下，其中的符號和參數見表1。

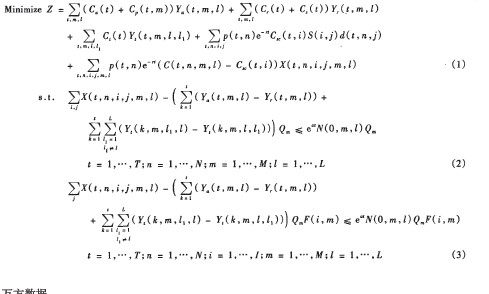
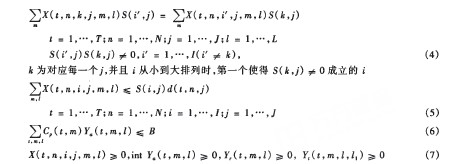
表1 模型中的符號和參數

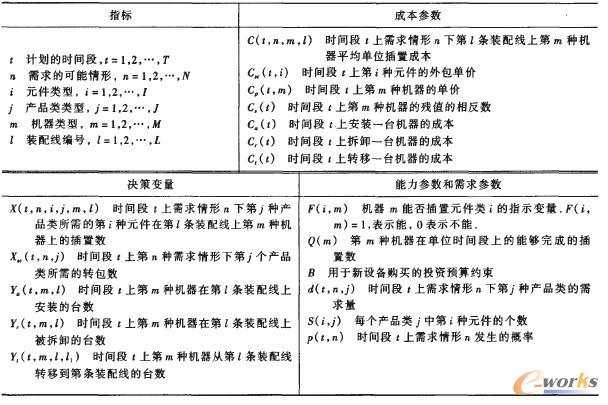
    上述模型加入了對于風險的描述，其中r是帶有風險的收益率(投資報酬率)，a為年期望風險收益率(風險貼水)，α = r－rf，rf為無風險利率。模型中(1)式為目標函數，前三項是裝配線的調整成本，分別對應于調整新機器、拆卸已有機器、轉移機器的成本，第四項和第五項為期望的外包成本和期望的生產成本之和。(2)式和(3)式為能力約束，分別要求每臺機器的總插置數不超過其總能力和第i種元件的生產計劃不超過每臺機器的能力。(4)式為BOM約束，要求每個產品類必須在同一條裝配線上完成，也即要求每條裝配線上產品類的元件生產計劃必須滿足BOM約束。(5)式為需求約束，要求每種元件的生產計劃不能超過需求。(6)式為投資預算約束，要求調整新設備的總投資不能超過預算。(7)式為非負和整數約束。

    模型M0是一個大規模混合整數規劃問題，一個實際的問題如18條裝配線用5類元件制造3個產品類，每條裝配線計劃期初平均有6臺插置機器，可選用的機器種類為40，計劃期(兩年)被等分為8個時間段(季度)，則模型有159，840個對應于生產計劃的連續決策變量，106，560個對應于裝配線調整的整數決策變量和297，224個約束．該模型無法直接進行求解。

3 減小搜索空間的略集求解方法

    如上節所述，一個實際的問題中含有106，560個能力調整整數決策變量，但是事實上可能只是某幾種機器加到某幾條裝配線上，也就意味著很多整數決策變量的值為零．一個直觀的解釋是，對于每一條裝配線，由于生產要滿足需求和成本約束以及產品類的BOM約束，同時考慮裝配線上已有的機器，某些種類的機器加到該條裝配線上是不可取的。因此可以通過一些啟發式算法把這些不可取的決策變量從搜索空間中去掉，本文先求解模型M0，得到一個對應于每個時間段每條裝配線需要加某些機器的集合(稱為增裝略集，略集中的每一個元素表示在某個時間段上某種機器加到某條裝配線是合適的)，然后應用一些規則對其進行修正，得到設備調整略集(包括增裝、拆卸以及轉移)，最后應用遺傳算法(GA)搜索調整略集以得到問題的一個近似最優解。

    用{A(t，m，Z)}表示時間段t上對應所有需求情形時第m種機器應該加到第z條裝配線上的集合，{B(t，n，m，L)}表示時間段t上對應每種需求情形rt時第m種機器應該加到第Z條裝配線上的集合，則集合{B(t，n，m，L)}可以通過類似于確定需求下增裝略集的求解方法得到(具體算法見文獻[11])．
    在得到{B(t，n，m，L)}之后，如何得到{A(t，m，L)}，一個直觀的方法如下：

     (8)式實際上是一種求所有市場需求情形下的最大的增裝略集的方法。

    在確定調整略集時，雖然求得的{A(t，m，L)}是一個增加機器的集合，但是在多計劃期時在該略集下求解，仍然會出現拆卸機器的情況，一個直觀的原因是由于開始的計劃期增加了較多的某種機器而導致后期的時間段上需要拆卸．基于這個原因，需要對集合{A(t，m，L)}作如下的修正：在確定每個時間段的調整略集時，都使它包含以前各期略集中相應的元素．同時由于求得的{B(t，n，m，L)}是每個時間段t上每種需求情形n下應該增加的機器集合，無法得到該時間段上該需求情形下應該拆卸的機器集合．解決這個問題的一個方法是，由于在計劃期初存在一個初始的裝配線布局，而考慮到機器的拆卸只能是對應于某時間段上某條裝配線存在這種機器的情形，因此可以進一步的修正集合{A(t，m，L)：再在每個時間段集合的元素中，加入初始布局上存在的機器種類．做了上述兩次修正后，可以得到最終的集合{A(t，m，L)}必然也包含了需要拆卸機器的集合．由于初始的裝配線布局對于機器種類也是稀疏的，作如上的處理雖然會使問題的規模仍然較大，但是相比較原始問題而言，它仍然在很大程度上縮小了搜索空間。

    當模型M0。的調整略集確定后，可以通過求解新的模型M1。來得到近似最優解．模型。只需把肘。中的(7)式替換成：

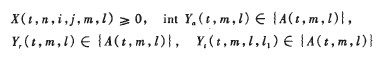
4 遺傳算法搜索調整略集

    應用遺傳算法搜索調整略集，以下將主要介紹算法的編碼方法和個體適應度評價方法，編碼方法：

    算法中染色體直接用0—20的十進制整數進行編碼，在每一位整數前加一個符號位，“－”表示拆卸機器，“+”則表示增加機器。生成初始群體時，考慮到不增加任何機器(對應染色體的所有基因位為零)是問題的一個可行解，而且考慮到最優解對應的染色體的很多基因位將會為零，算法中將不增加任何機器總是作為一個初始解。其他的初始解將由系統隨機生成，為了能夠確保隨機生成的初始解是問題的可行解，需要記錄每一期的裝配線結構，某一期的裝配線調整決策變量必須以上一期的裝配線結構為依據，只有當上一期裝配線包含某種機器，對應于該條裝配線的該種機器的基因才可能取負數，并且負數的絕對值不能超過原有機器的臺數；其他的基因只能隨機的取正數，這條原則在變異操作和交叉操作同樣需要遵循。

    個體適應度評價方法：

    記MIN和MAX分別為某一代染色體中所有染色體對應的模型肘．的目標函數值的最小值和最大值，本文定義如下地適應度函數：

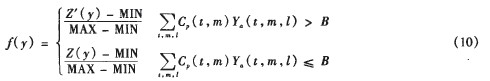
    在(10)式中，Zˊ(y)是模型M1的目標函數值上增加超過投資預算的適應性懲罰因子P(g，y)后的總成本，g為遺傳算法進化的代數，即

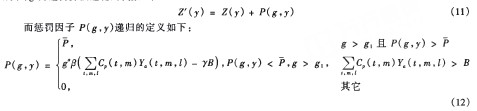
    在(12)式中，參數α≥0，β＞0，y，g1>1與P均是可調參數，用以調整懲罰因子的大小．其中，g，>l的作用在于算法開始的若干代不考慮投資預算約束．y的值可正可負，若取正，則相對而言有縮小超預算后果的作用，反之則有放大超預算后果的作用．參數α>0的作用在于對投資預算的約束隨進化代數的增加而要求越來越嚴厲。β>0是調整懲罰因子整體水平的參數，P為懲罰因子的上限。

    在上述的染色體中沒有基因位表示機器的轉移，但是實際上由于編碼時在整數變量前加了符號位，使得染色體中已經隱含了機器轉移的情況．考慮到模型的形式和求解順序，通過遺傳算法搜索解空間，得到一個表示機器增減的解串，此時生產能力調整已經確定，然后再在此能力調整方案下求解一個生產計劃問題(模型肘，的(2)式和(3)式)。

    若一個解串只是考慮增加或者減少機器兩種情況而不考慮機器轉移的情況，則通過(10)式確定的適應度函數值偏高，而對于模型肘。中生產能力的約束沒有影響．如對于某個時間段t某種機器m得到調整略集{A(t，m，1)，A(t，m，2)，A(t，m，4)}，即在第1、2、4條裝配線上需要調整機器m，在遺傳算法中用三個基因位表示。由于每個解串的每個基因位表示的是相應時間段相應裝配線上相應機器的增減情況，則在求解生產計劃問題時，只需要把這三個基因代入到能力約束((2)式和(3)式)中，即可得到時間段t上裝配線的實際布局，也即對于模型M1．中的生產能力約束沒有影響。

    若某個染色體中這三個基因分別為a，-b和C(其中a，b，C均為大于零的整數，并假定a>b)，則暗示著在一個實際的調整方案是將第m種機器從第2條裝配線轉移b臺到第1條裝配線上，實際調整成本：

    如果殘值按照購買單價的30％計算，則C—Cˊ<70％Cp(t，m)<0，即通過遺傳算法得到的適應度函數值偏高。同時可以看出，遺傳算法得到的投資成本也偏高．解決這個問題的一個方法是，在評價一個染色體的適應度時，首先識別略集中t和m相同的元素，并同時識別是否存在機器轉移的情況，如果存在，則需要根據(13)式計算生產能力調整成本以修正該染色體的總成本，并同時修正適應度函數值。

5 實例研究

    5.1 小規模仿真實例

    應用上述算法對隨機需求下的裝配線能力調整問題進行仿真計算．假設企業有2條生產線，共有3種機器可供選擇，生產的產品類為2種，且共有3種元件組成各種產品類，計劃期為2個(具體數據見文獻[11])。

    在上述的規模下，可以通過數學軟件LP_solver直接求解，用Y(t，m，L)表示第t時間段上第Z條裝配線第m種機器的調整臺數，y(t，m，L)為正表示增加，為負表示拆卸，則可以得到最優解如下：

    y(1，1，1)=1，y(1，1，2)=1，y(1，3，1)=3，y(1，3，2)=3，r(2，2，2)=-l，r(2，3，2)=-1，對應的總成本凈現值為$1600767。

    應用第三部分提出的方法求解得到的調整略集為(其中取δ=0.5)：A(1，1，1)，A(1，1，2)，A(I，2，2)，A(1，3，1)，A(1，3，2)，A(2，1，1)，A(2，1，2)，A(2，2，2)，A(2，3，1)，A(2，3，2)，其中一共有10個元素．再應用第四部分提出的遺傳算法搜索略集，得到的最優解為：y(1，1，1)=1，y(1，I，2)=1，y(1，3，1)=3，y(1，3，2)=3，r(2，2，2)=-1，g(2，3，2)=一1，對應的總成本凈現值為$1600767。

     從上述小規模仿真計算的結果可以看到，通過求取模型M。的調整略集，使得遺傳算法的搜索空間減少了(小規模問題減少了兩個元素，效果不是很明顯，但是對于大規模問題，搜索空間將會有較大幅度的減少)。同時可以看到通過計算得到的調整略集在減少搜索空間的同時能夠較好的保持搜索空間的完整性，從而提高了算法收斂到最優解的可能性。

表2 生產線初始布局

    5.2 大規模的仿真實例

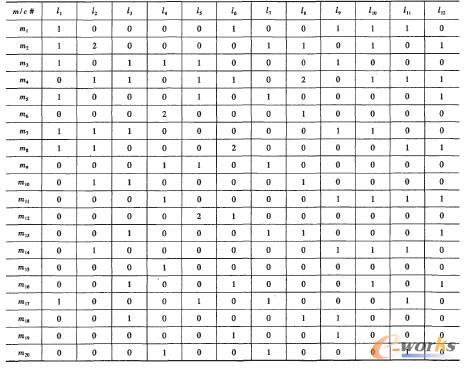
    某企業有12條生產線生產3個產品類．初始生產線布局如表2所示，共有20種機器可供選擇，其特征如表3所示，產品類結構如表4所示，市場需求如表5所示，各種市場需求情形出現的概率如表6所示．根據論文[11]的略集求解方法得到機器增裝略集如表7所示。

表3 可用機器特征

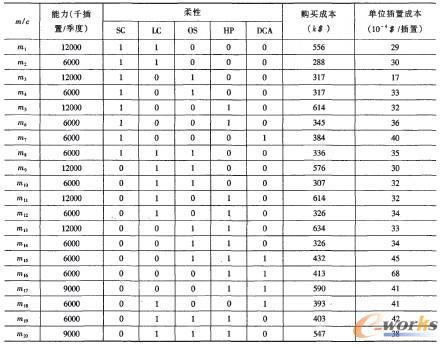
表4 產品類結構

表5 多時間段上市場需求情形

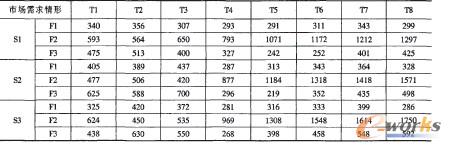
表6 各市場需求情形出現的概率

表7 時間段上的增裝略集

    應用本文提出的修正方法對增裝略集進行修正得到設備調整略集，然后在相同的條件下進行十次計算，得到的十個收斂解中最差的個體對應的生產線調整決策如下(對應的總成本凈現值為$31772412．oo)：

    Y(1，2，4)=2，y(1，3，7)=10，Y(2，14，2)=1，Y(6，3，5)=7，y(6，3，7)=1，l，(7，3，2)=3，y(7，3，4)=5，Y(8，3，12)=1。

    最優的個體對應的生產線調整決策如下(對應的總成本凈現值$31720234.00)：

    y(1，2，7)=3，l，(1，3，4)=4，l，(3，3，7)=5，y(4，3，7)=2，y(5，3，4)=6，y(5，3，5)=4，l，(6，3，8)=1．在上述實例中，十組解中目標函數值之間的最大誤差為0．16％，可以認為已經收斂到了近似解，于是我們把這個最優個體作為企業最后的生產線調整策略。

    5.3 算法的優越性

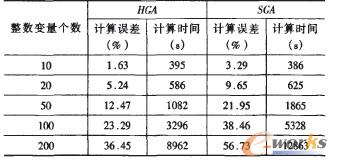
    由于本文建立的生產能力調整模型是一個大規模的混合整數規劃模型，目前還沒有較好的方法進行求解，在已有文獻中，標準遺傳算法是一種較為常用的求解這一問題的方法．因此，我們將從計算時間和計算誤差兩個方面，把本文算法(記為HGA)的結果與標準遺傳算法(記為SGA)的結果進行比較，以說明本文算法的適用性以及優越性．比較結果見表8，其中計算誤差的計算方法為：當整數變量個數小于20時，原問題可以通過數學軟件LP 80lvelr直接求解，此時最優解對應的最優值記為OPT，計算結果記為z(x)，則計算誤差為：(z(x)一oFr)／OPT×100．當整數變量個數大于20時，由于此時無法得到原問題的最優解，因此通過LP solver求解忽略整數約束時的線性規劃問題，得到最優解對應的最優值記為LB，則計算誤差為：(z(x)—LB)，OPT×100．由于LB是原始問題最優值的下界，因此，算法的實際誤差要低于該計算誤差。

    表8的計算結果顯示：雖然本文的算法處理規模較小的問題時，計算時間與標準遺傳算法相比不具有明顯的優勢(這主要是因為本文的算法在求解調整略集時需要花費一定的時間)，但是在計算精度上仍然要高于標準遺傳算法。而當問題規模較大時(整數變量個數大于50)，本文的算法無論在計算精度上還是計算時間上都遠遠優于標準遺傳算法，這說明了本文算法處理大規模混合整數規劃問題的有效性以及優越性。

表8 不同規模的計算結果比較

6 結論

    本文針對印刷裝配板的制造過程，建立了一個基于多種需求狀態的多計劃期多種產品類的能力規劃模型，該模型考慮了機器的柔性、產品類的BOM約束以及進行生產能力調整的風險。由于模型是一個大規模的混和整數規劃問題，無法用一般的數學軟件直接進行求解，本文提出了一種求解近似最優解的方法。首先減少裝配線能力調整決策變量的搜索空間，然后應用遺傳算法進行搜索．最后通過實例分析驗證了該方法的可行性，并將計算結果與標準遺傳算法的計算結果進行了比較。比較結果表明，相對于標準遺傳算法而言，盡管該方法在處理小規模問題時不具有顯著的優勢，但是在處理大規模問題時，該方法在計算精度上以及計算時間上都遠遠優于標準遺傳算法．因此，本文給出了一種處理大規模的多需求狀態下多計劃期多種產品類的能力規劃問題的有效方法，為企業制定相應的能力規劃決策提供了有力的支持。

核心關注：拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用，蘊涵了豐富的ERP管理思想，集成了ERP軟件業務管理理念，功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理，全面涵蓋了企業關注ERP管理系統的核心領域，是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。

轉載請注明出處：拓步ERP資訊網http://m.guhuozai8.cn/

本文標題：印刷裝配板行業ERP系統考慮BOM的FMS生產線能力規劃問題

本文網址：http://m.guhuozai8.cn/html/consultation/1082003716.html